Over the years various papers have been published aiming to quantify the heat transfer coefficient to easily measured or derived engine parameters. Some of the most common functions used are implemented in the combustion analysis software and are presented below.
Hohenberg1
`h=129.8V^(-0.06)p^(0.8)T^(-0.4)(bar v_p+1.4)^(0.8)` (Equation 1)
Woschni2
`h=129.8B^(-0.2)p^(0.8)T^(-0.53)(C_1 bar v_p+C_2 (V_s T_(ref))/(p_(ref) V_(ref)) (p-p_("motored")))^(0.8)` (Equation 2)
where:
C1 = 6.18 in scavenging period
C1 = 2.28 in compression, combustion and expansion
C2 = 0 in scavenging period and compression
C2 = 3.24 x 10-3 in combustion and expansion
C2 = 6.22 x 10-3 in combustion and expansion (IDI engines)3
Annand4
`h=(a lambda)/B Re^(0.7)+c (T^4 - T_(wall)^4)/(T-T_(wall))` (Equation 3)
where:
0.35 < a < 0.8
c = 0 during intake and compression
c = 0.576σ for CI engine combustion and expansion
c = 0.075σ for SI engine combustion and expansion
from Bosch5 σ = 5.67 x 10-8 W.m-2.K-4
from Street et al6
`Re=(V d rho)/mu` (Equation 4)
where:
V is the mean velocity in the pipe (mean piston speed) in metres per second
d the characteristic length (engine bore) in metres
ρ is the density of the fluid in kilograms per cubic metres
μ is the dynamic fluid viscosity in kilograms per metre per second
Mean piston speed is calculated from engine speed:
`V=2 L N` (Equation 5)
where:
N is engine speed in revolutions per second
L is engine stroke in metres
`rho=p/(RT)` (Equation 6)
Annand4 approximates:
`lambda=(C_p mu)/0.7` (Equation 7)
from Brunt7:
`C_p=R/(1-(1/gamma))` (Equation 8)
`gamma=1.338-6.0*10^(-5)T+1.0*10^(-8)T^2` (based on gasoline engine) (Equation 9)
The following figures are published:
Brunt:
a=0.45
R=288.8
Annand:
mu=4.702 x 10-7.T0.645 (Equation 10)
R=241.1
The validity of Annand's equation for dynamic fluid viscosity, equation 7, is compared in figure 1 to published figures. It is noted from the sources of the published values8,9,10 that μ does not vary significantly with pressure.
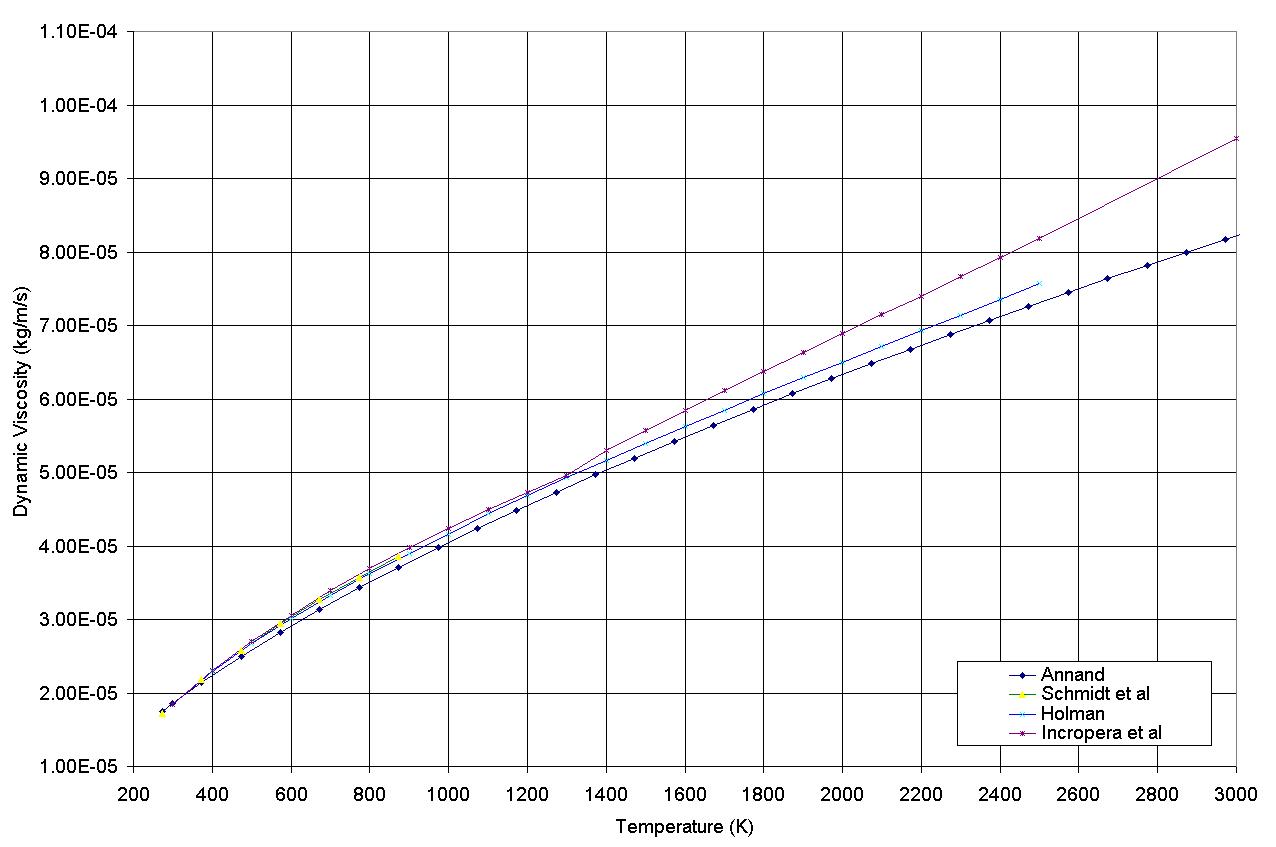
Figure 1 - Published values of the dynamic viscosity of air
It should be noted that the equations developed to calculate heat transfer coefficient are derived empirically from heat flux measurements. Therefore, the equations are only valid for the type and geometry from which they are derived.
Heat transfer coefficient formulas are used because it is impractical to derive accurate formula for every engine under investigation and because the differences between coefficients calculated by different formulae do not provide substantially different final results. The choice of which heat transfer coefficient to use, should be down to the particular application and whether data is being compared to data calculated using a particular method.
catool Implementation: See Return_Heat_Release_Data() in analysis.c
References:
1. Hohenberg, G., "Advanced Approaches for Heat Transfer Calculations," SAE Paper 790825, 1979.
2. Woschni, G., "A Universally Applicable Equation for the Instantaneous Heat Transfer Coefficient in the Internal Combustion Engine," SAE Paper 670931, 1967.
3. Stone, R., "Introduction to Internal Combustion Engines," Macmillan Press Limited, Basingstoke, Hampshire, 1999.
4. Annand, W. J. D., "Heat Transfer In The Cylinders Of Reciprocating Internal Combustion Engines," Proc. I. Mech. E., Vol. 177, No. 36, pp. 973-989, 1963.
5. Robert Bosch GmbH, "Automotive Handbook: Second Edition," Stuttgart, Germany, 1986.
6. Street, R., Watters, G., Vennard, J., "Elementary Fluid Mechanics: Seventh Edition," John Wiley & Sons, Inc., New York, USA, 1996.
7. Brunt, M. F. J., Rai, H., Emtage, A. L., "The Calculation of Heat Release Energy from Engine Cylinder Pressure Data," SAE Paper 981052, 1998.
8. Schmidt, F. W., Henderson, R. E., Wolgemuth, C. H., "Introduction to thermal sciences," John Wiley and Sons, New York, 1993.
9. Holman, J. P., "Heat Transfer, 8th edition," McGraw-Hill, Inc., New York, 1997.
10. Incropera, F. P., de Witt, D. P., "Introduction to Heat Transfer: Second Edition," John Wiley and Sons, New York, 1990.